“Khối đa diện” là một trong 2 chuyên đề oái oăm và khó nhằn trong hình học không gian đối với rất nhiều bạn học sinh. Tuy nhiên, nhìn theo hướng tích cực thì chính những chuyên đề thuộc loại “khoai” này mới có thể giúp bạn tạo ra khoảng cách điểm số với “đối thủ”. Để học tốt chuyên đề này bạn nhất định phải biết những lưu ý dưới đây:
Chuyên đề: Khối đa diện
1.Tập trung vào lý thuyết
Không có con đường nào khác giúp bạn giải được bài toán oái oăm về khối đa diện mà không hiểu rõ bản chất của nó. Để hiểu rõ bản chất thì bạn phải nắm chắc và hiểu rõ những khái niệm, định nghĩa, công thức tính… Tuyệt đối không xem nhẹ lý thuyết. Lý thuyết sẽ giúp bạn vẽ hình trăm phát đúng cả trăm và biết cách tính toán đúng nhất. Thêm nữa, đề thi minh họa và thử nghiệm Bộ GD&DT ra đều có câu hỏi lí thuyết phần này nên nắm chắc lý thuyết sẽ giúp bạn ghi điểm trực tiếp trong đề thi THPT quốc gia 2017.
- Vận dụng trí tưởng tượng
Muốn làm được hình học không gian, điều tiên quyết là phải vẽ hình đúng bằng việc vận dụng trí tưởng tượng.Tưởng tượng như thế nào? Ít nhất là khi đọc được 1 đề bài bạn phải nghĩ ngay ra đó là hình gì và vẽ chúng như thế nào, vẽ mặt nào ra ngoài để dễ nhìn hình. Bạn sẽ nhìn được rõ ràng các góc, các mặt mà mình cần tính toán ngay.
3. Nắm được các công thức
Điều hiển nhiên để làm được bài tập thì tất tần tật công thức bạn phải nắm chắc từ tính thể tích hình chóp, thể tích hình lăng trụ đến các công thức về diện tích các hình, các hệ thức lượng trong tam giác, định lí sin, định lí cosin….
Dưới đây là một số sơ đồ tư duy của Thầy Nguyễn Thanh Tùng-giáo viên dạy Toán tại HOCMAI đã “kỳ công” sáng tạo giúp cho các bạn học sinh dễ hiểu và dễ nắm công thức hơn.
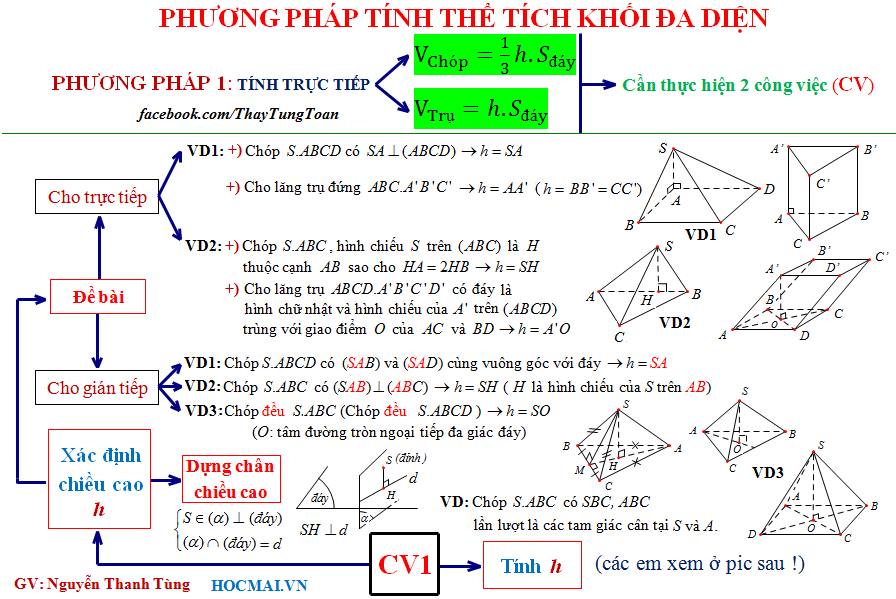
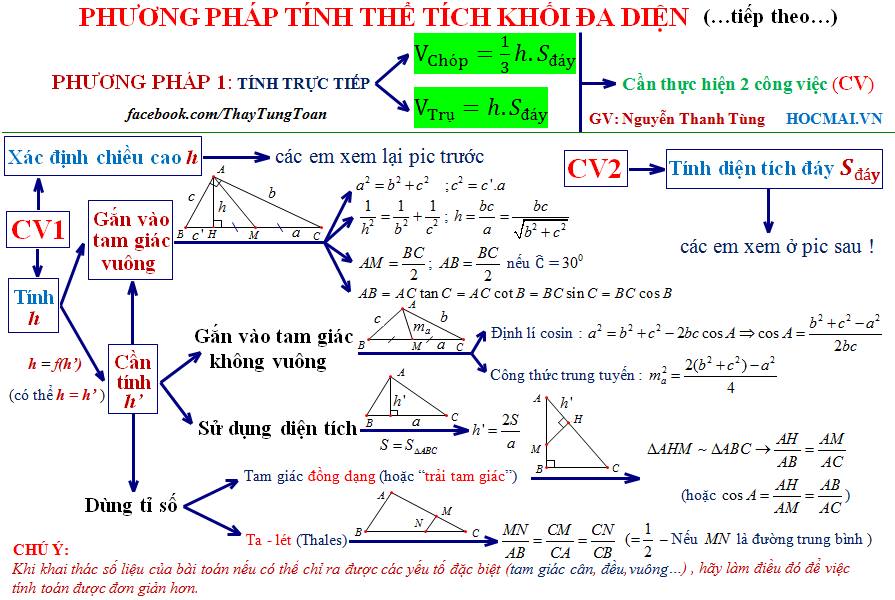
Thầy Nguyễn Thanh Tùng-chủ nhân của tất cả sơ đồ tư duy trong bài
4. Nắm được cách xác định mọi loại góc, khoảng cách trong hình học không gian
Trong hình học không gian có rất nhiều dạng bài tìm khoảng cách: khoảng cách từ 1 điểm đến 1 đường thẳng, khoảng cách từ 1 điểm đến một mặt phẳng, khoảng cách giữa 2 đường thẳng chéo nhau. Cách xác định góc giữa hai đường thẳng,góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng.
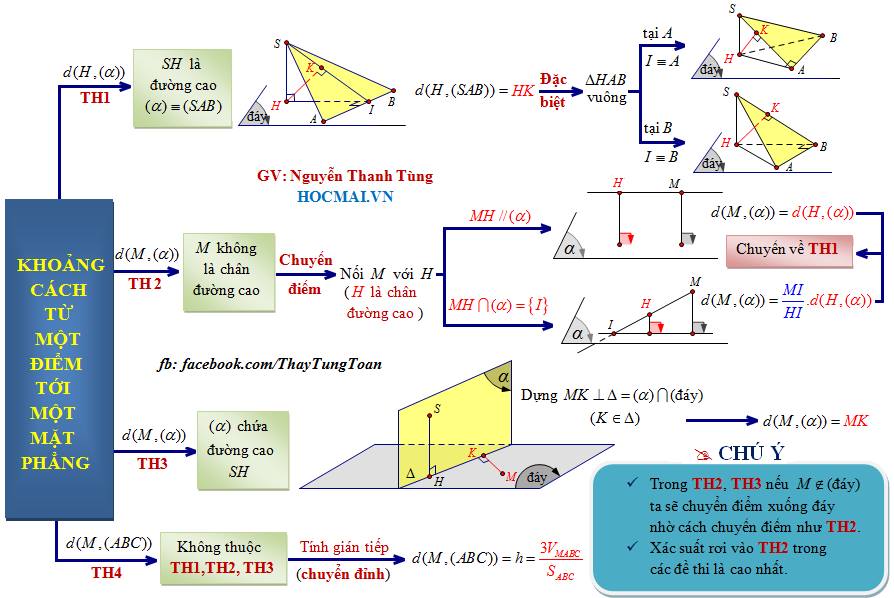
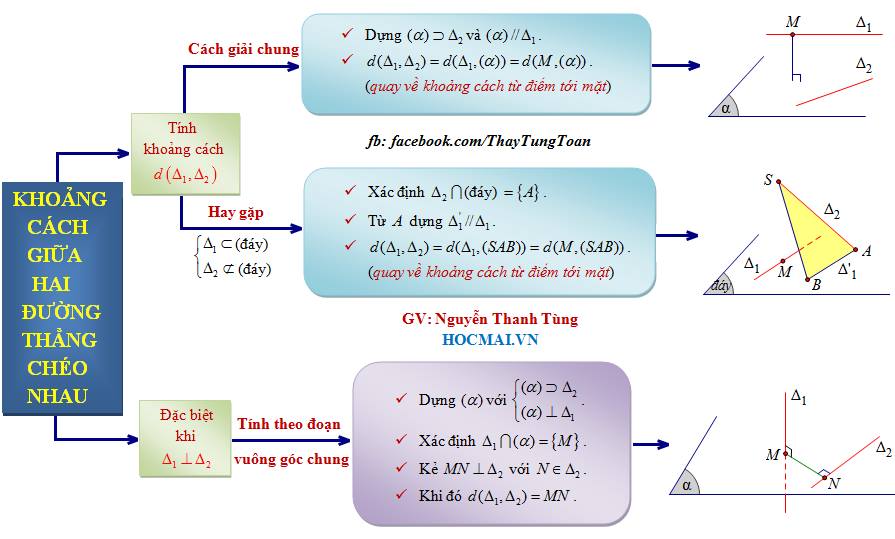
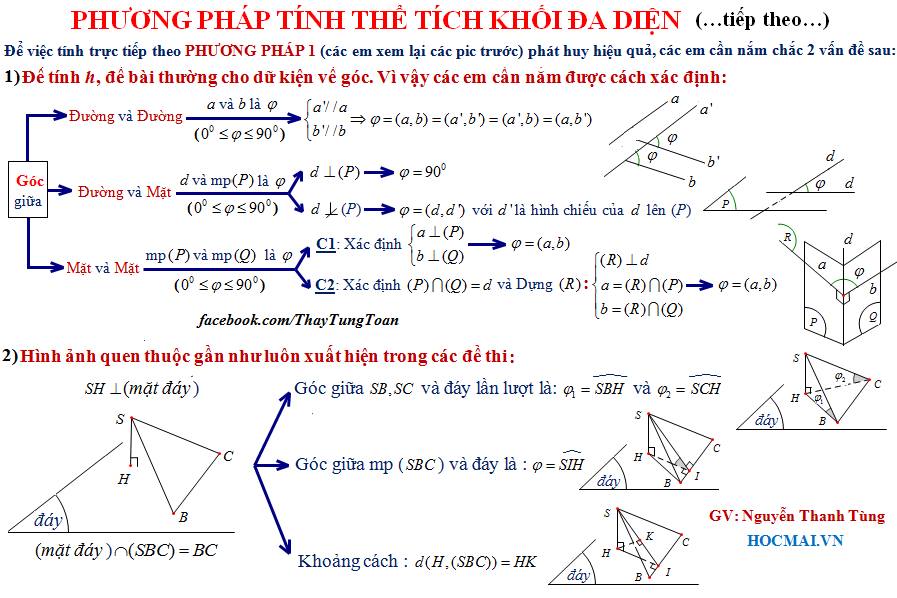
Để làm được những dạng bài toán trong hình học không gian điều bạn cần không chỉ chăm chăm luyện nhiều bài tập mà bạn nhất định cần có phương pháp giải hay, những lưu ý TƯỞNG NHỎ NHOI mà CỰC QUAN TRỌNG để tránh mất điểm oan với những lỗi học sinh nào cũng mắc phải.
HOCMAI miễn phí nhiều khóa học bổ trợ – đề thi thử – phương án học tập và ôn luyện bứt phá 9+ đanh cho học sinh lớp 1-12. Tải & hoàn thành đăng ký tài khoản để nhận ngay những khóa học bổ trợ miễn phí!
