Giới hạn của hàm số rất quan trọng vì liên quan nhiều đến phần đạo hàm, tích phân ở lớp 12. Xem ngay bài viết dưới đây để chinh phục ‘giới hạn của hàm số’ với thầy Lưu Huy Thưởng nhé!
Trong bài viết trước (gắn link), thầy Lưu Huy Thưởng đã hướng dẫn các bạn cách học phần ‘giới hạn của dãy số’, hôm nay thầy sẽ tiếp tục với phần ‘giới hạn của hàm số, các bạn cùng xem nhé!
Lý thuyết cần nhớ
Cũng như giới hạn của dãy số, các em chỉ cần nhớ một bảng này thôi là sẽ nắm được toàn bộ lý thuyết phần này.
5 dạng toán thường gặp và phương pháp giải
Phần giới hạn của hàm số có nhiều dạng bài hơn, các em cần phải nắm được tất cả 5 dạng nhé!
Dạng 1: Dạng cơ bản
Tìm các giới hạn sau
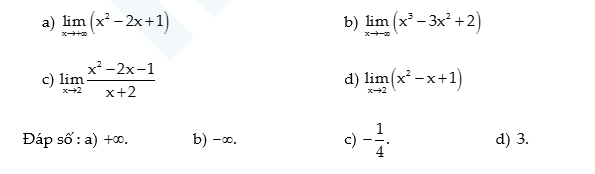
Dạng 2: Dạng vô định (0/0)
Phương pháp:
- Phân tích cả tử và mẫu thành nhân tử rồi rút gọn.
- Sử dụng các hằng đẳng thức đáng nhớ để nhân lượng liên hợp ở tử và mẫu.
Dạng 3: Dạng vô định (vô cùng/ vô cùng)
Phương pháp:
- Nếu P(x), Q(x) là các đa thức thì chia cả tử và mẫu cho luỹ thừa cao nhất của x.
- Nếu P(x), Q(x) có chứa căn thì có thể chia cả tử và mẫu cho luỹ thừa cao nhất của x hoặc nhân lượng liên hợp.
- Nếu bậc của tử nhỏ hơn bậc của mẫu thì kết quả của giới hạn đó bằng 0.
- Nếu bậc của từ bằng bậc của mẫu thì kết quả của giới hạn đó bằng tỉ số các hệ số của luỹ thừa cao nhất của tử và của mẫu.
- Nếu bậc của tử lớn hơn bậc của mẫu thì kết quả của giới hạn đó là +vô cùng nếu hệ số cao nhất của tử và mẫu cùng dấu và kết quả là – vô cùng nếu hệ số cao nhất của tử và mẫu trái dấu.
Dạng 4: Dạng vô định (vô cùng – vô cùng)
Phương pháp: Ta thường sử dụng phương pháp nhân lượng liên hợp của tử và mẫu. Một số trường hợp có thể rút x.
Dạng 5: Giới hạn một bên (0.vô cùng)
Nếu các em vẫn còn yếu lý thuyết hay vẫn chưa thành thạo cách giải bài tập, hãy xem giải pháp đem lại ưu thế trong kỳ thi THPT 2018 chỉ sau 4 tháng học với chi phí chỉ tương đương 30k/1 tháng TẠI ĐÂY
“Xây nền vững vàng, luyện thi cực nhàn”
HOCMAI miễn phí nhiều khóa học bổ trợ – đề thi thử – phương án học tập và ôn luyện bứt phá 9+ đanh cho học sinh lớp 1-12. Tải & hoàn thành đăng ký tài khoản để nhận ngay những khóa học bổ trợ miễn phí!
